Scalable Multi-Agent Reinforcement Learning for Collision Avoidance

This work is part of my Mater’s Thesis at the Royal Institute of Technology (KTH), Stockholm, Sweden (URL available soon). The scalable part of this work is inspired by the paper Scalable Reinforcement Learning for Multi-Agent Networked Systems. The approach presented on the thesis exploits the structure of the designed reward to present $\Delta$-disk local approximation of the individual Q functions and policy gradients.
Important Scripts
- drone_env.py: Script containing the environment class and its methods. The main methods follow the structure of the OpenGym RL environments, such as
.step()and.reset(). - train_problem.py: Script containing the training of the main problem.
- SAC_agents.py: Script containing the agent classes and its policy classes
- benchmark_agent.py: Scripts to run trained agents and benchmark their performance
Training of the scalable agents
The schema of the algorithm used is presented below. The scalable actor-critic agents are trained for each robotic agent. There are a total of n agents.

Structure of the training script

Relevant results
Softmax discrete policy
The individual policy for each agent is of the shape:

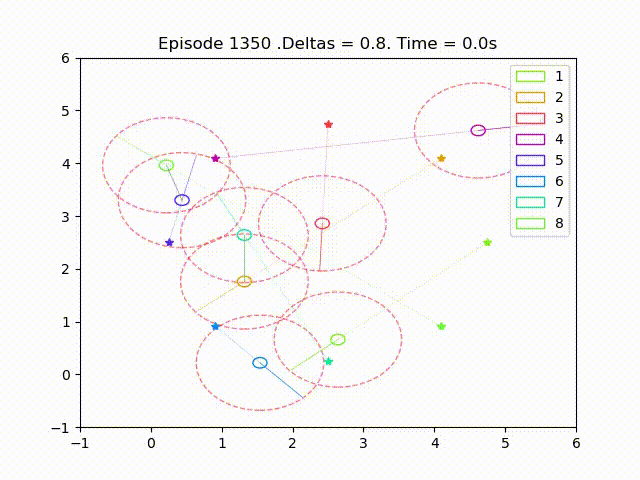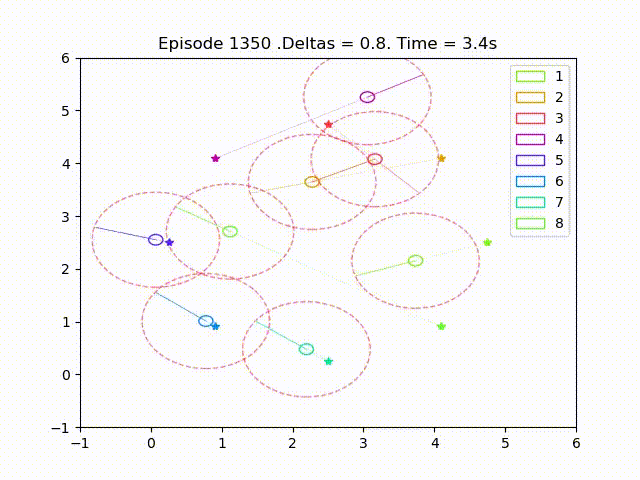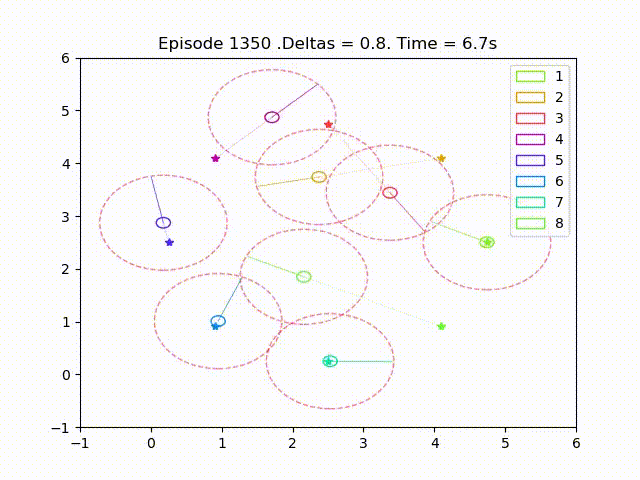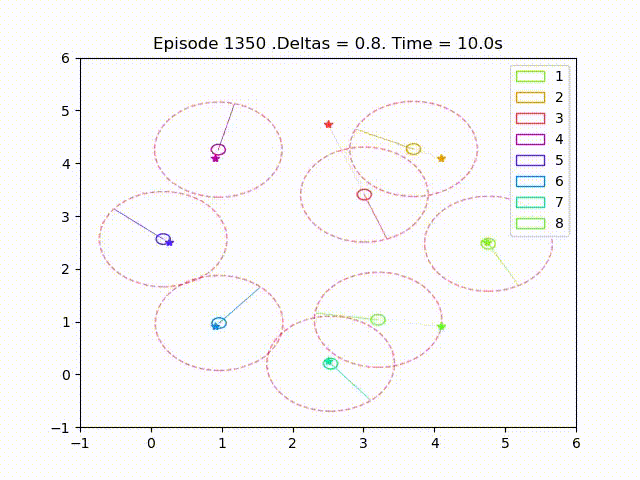
Some examples of trajectories obtained after successful training are as follow

Continous normally distributed policy
The individual policy for each agent is of the shape:

Some examples of trajectories obtained after successful training are as follow

Comparison of tested policies
The number of collisions displayed on the results are defined as an agent intersection with a neighbour’s collision radius in a given time step. Each agent counts collisions separately, thus two agents colliding is counted as two different collisions and a collisions that lasts for several times steps is is also counted as different collisions.
Percentage of simulations that achieve each number of collisions for each of the three tested policies, n = 5. The percentages for more than 14 collisions (under 1%) have been omitted.

Effect of the ∆-disk radius (definition 12 on the thesis) on the global reward and number of collisions, averaged over 2000 runs of the trained policies, for the discrete softmax NN policy

The results also show that the average reward starts to decrease after a certain value of $ \Delta_i $ , in this case around 1. The average number of collisions also increases sharply back to values where the agent has nearly no vision. This unexpected behaviours is the result of significant increase in the complexity of the maximization problem that the policy gradient is trying to solve. Taking into account an increasing number of neighbours and from further distances, increases the variance of the estimated approximated gradient and as a result, the policy used is not able to find improvements. Indeed, for the final case of $ \Delta_i \approx \hat{d}_{i} $ is not able to converge during training.